Het model van een (gedempte) trilling.

Het model van een (gedempte) trilling.#

In deze opdracht wordt een model van een trilling uitgebreid met demping op twee manieren en deze opdrachten bevat diverse vragen geschikt voor een cijfer.

import numpy as np              #importeer bibliotheek numpy
import matplotlib.pyplot as plt #importeer matplot
%matplotlib inline
#De laatste regel zorgt dat de plots in het notebook komen en niet popuppen.

Model van een trilling zonder demping#

We maken eerst een eenvoudig model voor een trilling aan de hand van een massa-veer systeem. Bij dit model zijn de volgende startwaarden nodig: (druk op play/run)

t=0
dt = 0.001
m = 0.1
C = 500 #veerconstante in N/m
v=0
x=-0.1
eindtijd =2

Technische info:
Het model wordt hieronder met een ‘while’ lus gemaakt. Zolang de tijd kleiner is dan de eindtijd blijft de lus doorgaan. We willen later een grafieken voor de snelheid en de plaats als functie van de tijd maken. Hiervoor moeten eerst (lege) lijsten (tabellen) gemaakt worden.
Begrijp je dit bovenstaande niet helemaal, geen ramp.

Het model:
Het model wordt in het code blok hieronder heel duidelijk aangegeven door #begin model en #eind model. Dit zijn de eigenlijke modelregels, dit zou je moeten begrijpen, en dit is de plek waar je later dingen kan aanpassen, en nergens anders. Let erop dat alles netjes onder elkaar blijft staan. Bekijk het code blok en druk vervolgens op het run knopje.
Het eerste model is een model van een trilling zonder demping.

tijden = [t] # de lijst 'tijden' met een begintijd is gemaakt
snelheden = [v] # en 'snelheden'
plaatsen = [x] # en 'plaatsen' ook

while t < eindtijd:
    # begin model
    t = t + dt
    Fv = -C * x
    a= Fv / m
    dv = a * dt
    v = v + dv
    dx = v * dt
    x = x + dx
    # eind model

    # begin van het vullen van de lijsten
    snelheden.append(v) # voegt een snelheid toe aan de lijst met snelheden.
    plaatsen.append(x) # voegt een plaats toe aan een lijst met plaatsen.
    tijden.append(t) # voegt de tijd toe aan een lijst met tijden.
    # eind van het vullen van lijsten

Nu maken we grafieken (plotten). Druk op run om ze te laten verschijnen. Eerst het v-t diagram:

plt.figure(figsize=(10,10))
plt.plot(tijden, snelheden, 'b')
plt.title('De snelheid als functie van de tijd')
plt.xlabel('tijd [s]')
plt.ylabel('snelheid [m/s]')
plt.grid()
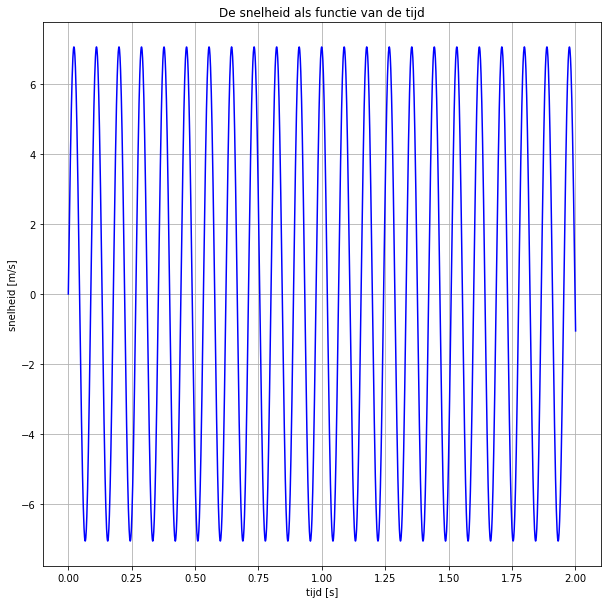
../_images/9a0c74c592a5c4080bb8f72ae37064b1f372327183ee4b241e10ff963d4f7e2e.png

En nu maken we de x-t grafiek. Druk op run om te laten verschijnen:

plt.figure(figsize=(10,10))
plt.plot(tijden, plaatsen)
plt.title('De plaats als functie van de tijd')
plt.xlabel('tijd [s]')
plt.ylabel('uitwijking [m]')
plt.grid()
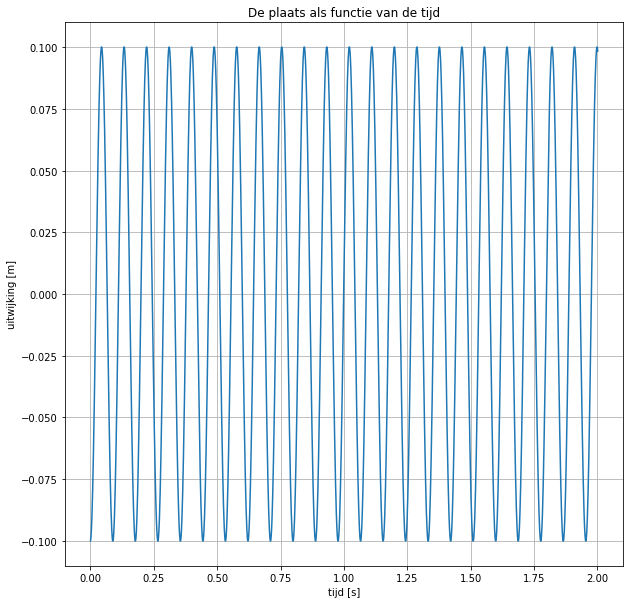
../_images/684fc92486eebbaf1d4fd8f617c304c8c9ac0eee4b974c19124936ecd491e568.png

Hierboven staat alle uitleg en het basismodel.

Nu komen de eigenlijke opdrachten:#

OPDRACHT 1: Leg mbv het model uit dat de resulterende kracht en de uitwijking tegengesteld gericht zijn.

Type hier je antwoord: (even dubbelklikken)

OPDRACHT 2: Bereken met mbv de startwaarden de T.

Type hier je antwoord:

OPDRACHT 3: Bepaal T ook op grond van het bovenstaande model en bereken de eventuele procentuele afwijking.

Type hier je antwoord:



We beschouwen nu ene nieuwe situatie met een andere veer. Deze veer heeft een veerconstante van 10 N/m, er zit een massa aan van 50 gram en de veer wordt 10 cm ingedrukt voordat de veer begint te trillen.

OPDRACHT 4: Vul de startwaarden hieronder aan, zodat aan deze nieuwe situatie wordt voldaan.

t=0
dt = 0.001
m =
C =
v=
x=
eindtijd =10

##Model met eenvoudige demping Hieronder staat het basismodel (behorende bij de eerste 3 opdrachten) van boven hier nogmaals.
Het model is nu nog niet realistisch genoeg omdat het nooit stopt zonder stop voorwaarde. Dat komt omdat er geen rekening is gehouden met wrijving of demping van de veer. Voor de demping van een veer geldt een theoretisch model.
Demping door sleepwrijving ook wel vloeistofwrijving genoemd:

wrijvingskracht = constante (c2) x snelheid

OPDRACHT 5: Voeg deze wrijvingskracht toe aan het model hieronder. Vul hiertoe model code aan op de …. hieronder in het model. Als je wilt kun je de code blokken runnen om ze te controleren.

startwaarden:

t=0
dt = 0.001
m = 0.1
C = 500 #veerconstante in N/m
c2 = 1.5
v=0
x=-0.1
eindtijd =2

model simulatie:

tijden = [t] # de lijst 'tijden' met een begintijd is gemaakt
snelheden = [v] # en 'snelheden'
plaatsen = [x] # en 'plaatsen' ook
while t < eindtijd:

    # begin model
    t = t + dt
    Fv = -C * x
    Fw = .....
    Fres= Fv .....
    a=Fres / m
    dv = a * dt
    v = v + dv
    dx = v * dt
    x = x + dx
    # eind model

    # begin van het vullen van de lijsten
    snelheden.append(v) # voegt een snelheid toe aan de lijst met snelheden.
    plaatsen.append(x) # voegt een plaats toe aan een lijst met plaatsen.
    tijden.append(t) # voegt de tijd toe aan een lijst met tijden.
    # eind van het vullen van lijsten

grafiek v-t

plt.figure(figsize=(10,10))
plt.plot(tijden, snelheden, 'b')
plt.title('De snelheid als functie van de tijd')
plt.xlabel('tijd [s]')
plt.ylabel('snelheid [m/s]')
plt.grid()

grafiek x-t

plt.figure(figsize=(10,10))
plt.plot(tijden, plaatsen)
plt.title('De plaats als functie van de tijd')
plt.xlabel('tijd [s]')
plt.ylabel('uitwijking [m]')
plt.grid()

OPDRACHT 6: Pas het model zodanig aan dat de trilling tussen 0,75 en 1,0 seconde geheel gedempt is.

##Model met extra demping Het model met demping hierboven is nog niet ideaal. Het houdt geen rekening met demping door luchtwrijving. Het model hieronder doet dit wel.

startwaarden:

t=0
dt = 0.001
m = 0.1
C = 500 #veerconstante in N/m
C2 = 0.1
C3 = 0.1
v=0
x=-0.1
teken=1
eindtijd =2

simulatie van model:

tijden = [t] # de lijst 'tijden' met een begintijd is gemaakt
snelheden = [v] # en 'snelheden'
plaatsen = [x] # en 'plaatsen' ook
while t < eindtijd:
    # begin model
    t = t + dt
    Fv = -C * x
    Fw = teken * c2 * v ** 2   # Demping door luchtwrijving -- de sterretjes ** 2 betekenen macht van 2.
    Fres=Fv - Fw
    a=Fres / m
    dv = a * dt
    v = v + dv
    dx = v * dt
    x = x + dx
    if v<0:                   #if betekent ALS
      teken=-1
    else:                     #else betekent ANDERS of EIND-ALS
      teken=1
    # eind model
    # begin van het vullen van de lijsten
    snelheden.append(v) # voegt een snelheid toe aan de lijst met snelheden.
    plaatsen.append(x) # voegt een plaats toe aan een lijst met plaatsen.
    tijden.append(t) # voegt de tijd toe aan een lijst met tijden.
    # eind van het vullen van lijsten

grafiek v-t:

plt.figure(figsize=(10,10))
plt.plot(tijden, snelheden, 'b')
plt.title('De snelheid als functie van de tijd')
plt.xlabel('tijd [s]')
plt.ylabel('snelheid [m/s]')
plt.grid()

grafiek x-t:

plt.figure(figsize=(10,10))
plt.plot(tijden, plaatsen)
plt.title('De plaats als functie van de tijd')
plt.xlabel('tijd [s]')
plt.ylabel('uitwijking [m]')
plt.grid()

OPDRACHT 7: Leg uit waarom in dit model gebruik wordt gemaakt van “teken” om de wrijvingskracht te berekenen. Betrek in je antwoord de voorwaarde voor “teken” die opgenomen is in het model, als ook waarom de resulterende kracht op deze manier wordt berekent.

Type hier je antwoord:

OPDRACHT 8: Er is geen sinusfunctie in het model ingevoerd en toch komt er telkens een sinus uit.
Verklaar dat aan de hand van de theorie.

Type hier je antwoord:

##Model met zwaartekracht OPDRACHT 9: Pas het model hieronder zodanig aan dat er rekening wordt gehouden met de zwaartekracht. (dus dat de veer hangt, ipv op zijn zij ligt). Doe dit in het model hieronder:

startwaarden:

t=0
dt = 0.001
m = 0.1
C = 500 #veerconstante in N/m
C2 = 0.1
C3 = 0.1
v=0
x=-0.1
teken=1
eindtijd =2

simulatie van model:

tijden = [t] # de lijst 'tijden' met een begintijd is gemaakt
snelheden = [v] # en 'snelheden'
plaatsen = [x] # en 'plaatsen' ook
while t < eindtijd:
    # begin model
    t = t + dt
    Fv = -C * x
    Fw = teken * c2 * v ** 2   # Demping door luchtwrijving -- de sterretjes ** 2 betekenen macht van 2.
    Fres=Fv - Fw
    a=Fres / m
    dv = a * dt
    v = v + dv
    dx = v * dt
    x = x + dx
    if v<0:                   #if betekent ALS
      teken=-1
    else:                     #else betekent ANDERS of EIND-ALS
      teken=1
    # eind model
    # begin van het vullen van de lijsten
    snelheden.append(v) # voegt een snelheid toe aan de lijst met snelheden.
    plaatsen.append(x) # voegt een plaats toe aan een lijst met plaatsen.
    tijden.append(t) # voegt de tijd toe aan een lijst met tijden.
    # eind van het vullen van lijsten

grafiek v-t:

plt.figure(figsize=(10,10))
plt.plot(tijden, snelheden, 'b')
plt.title('De snelheid als functie van de tijd')
plt.xlabel('tijd [s]')
plt.ylabel('snelheid [m/s]')
plt.grid()

grafiek x-t:

plt.figure(figsize=(10,10))
plt.plot(tijden, plaatsen)
plt.title('De plaats als functie van de tijd')
plt.xlabel('tijd [s]')
plt.ylabel('uitwijking [m]')
plt.grid()

##Model met kinetische energie OPDRACHT 10:Pas het model hieronder zo aan, dat de kinetische energie wordt berekent en weergegeven in een grafiek.

startwaarden:

t=0
dt = 0.001
m = 0.1
C = 200 #veerconstante in N/m
v=0
x=-0.1
eindtijd =2
Ek=

simulatie van het model:

tijden = [t] # de lijst 'tijden' met een begintijd is gemaakt
snelheden = [v] # en 'snelheden'
plaatsen = [x] # en 'plaatsen' ook
kinEnergie = [Ek]

while t < eindtijd:
    # begin model
    t = t + dt
    Fv = -C * x
    a= Fv / m
    dv = a * dt
    v = v + dv
    dx = v * dt
    x = x + dx
    Ek =
    # eind model

    # begin van het vullen van de lijsten
    snelheden.append(v) # voegt een snelheid toe aan de lijst met snelheden.
    plaatsen.append(x) # voegt een plaats toe aan een lijst met plaatsen.
    tijden.append(t) # voegt de tijd toe aan een lijst met tijden.
    kinEnergie.append(Ek)
    # eind van het vullen van lijsten

grafiek v-t en Ek

plt.subplot(2, 1, 1)
plt.plot(tijden, snelheden, 'b')
plt.title('de snelheid en kinetische energie als functie van de tijd')
plt.ylabel('snelheid [m/s]')
plt.grid()
plt.subplot(2, 1, 2)
plt.plot(tijden, kinEnergie, 'g')
plt.xlabel('tijd [s]')
plt.ylabel('Ek [J]')
plt.grid()
plt.show()

OPDRACHT 11: Leg uit (als je opdracht 10 goed gedaan hebt) waarom de de grafiek van Ek 2x zoveel trillingen laat zien in de dezelfde tijd als die van de snelheid.

Type hier je antwoord: