LES 3: Functies en grafieken#
In het vorige onderdeel heb je geleerd hoe je functies kan definieren. Het heeft wat weg wat je met wiskunde een functie noemt: de wiskundefunctie f(x) = 3x + 2 heeft als input een x, en als output een getal f(x). Bij programmeren kan je ook andere objecten als input en output hebben, zoals tekst (strings) of lijsten.
Het voordeel van gebruik van functies is dat je ze maar 1x hoeft te bouwen en daarna in de rest van je programma opnieuw kan oproepen.
In dit hoofdstuk leer je wiskundige functies maken, en hoe je dit kan plotten in een grafiek.
Ter herhaling, de opbouw van een functie is als volgt:
def functienaam(variabele1, variabele2, ...): hiermee DEFinieer een functienaam waarin variabelen worden ingevoerd. Let op dat als je de functie later oproept, je de zelfde HOEVEELHEID variabelen in dezelfde VOLGORDE invoert zoals als je gedefinieerd hebt.
Eronder geef je een TAB en maak je de rest van het programma. je eindigt met return functieuitkomts , je wilt namelijk een output maken en moet je even aangeven wat je als output wilt. Dit kan een getal zijn, maar ook een string of een boleaanse waarde true of False.
Later in je code kan je dan door simpelweg functienaam(1,3) oproepen met jouw waarden voor variabele1 en variabele2 (hier 1 en 3) in te vullen en komt er een output uit die je later weer kan gebruiken.
In de code beginnen we eenvoudig met een rechte lijn. Je ziet dat het vrij bewerkelijks kan zijn. Probeer elke regel goed te snappen.
Hieronder maaken we een algemene rechte lijn y=ax+b, waarbij we als input moeten hebben de hellingsgetal a, de startgetal b. We moeten ook aangeven op welk domein “de x-waarden” we willen werken, en welke stapgrootte we willen. De input is dan een lijst van y-waarden. n. Er zijn nieuwe dingen bij gekomen dus lees het goed!
def lijn(a,b,xstart,xeind,stapgrootte): #we definieren een lijn met variabelen a, b, xstart, xeind en startgrootte
y=[xstart*a+b] # hier wordt een lijst gemaakt, genaamd y, waarbij alvast de eerste waarde alvast is ingevuld. Dit hoeft niet per se, maar dan moet je nadenken over je while loop hieronder.
x=[xstart] # dito voor de y maken we een lijst met de xwaarden. Is nu gedaan voor later als we grafieken gaan tekenen
xwaarde = xstart # hier wordt een variabele gedefinieerd, die we in de formule y=ax+b willen invoeren. We beginnen met de rand van het domein (xstart)
while xwaarde < xeind: # zolang de rechterrand (xeind) nog niet is bereikt, berekenen we de waarden van y:
xwaarde = xwaarde+stapgrootte # eerst de eerstvolgende xwaarde
ywaarde = a*xwaarde +b # dan de y-waarde bij x-waarde met y=ax+b
x.append(xwaarde) # vul dan het lijstje x aan met de xwaarden
y.append(ywaarde) # vul dan het lijstje y aan met de ywaarden
return y # de output van deze functie
lijn(3,2,-3,4,0.1) # hier wordt de boven gedefinieerde functie aangeroepen en de 5 variabelen achtereenvolgens gedefinieerd. De output zal zijn de de y-waarden bij de functie y=3x+2 van x=-3 tot x=4 met stapgrootte 0.1.
[-7,
-6.699999999999999,
-6.399999999999999,
-6.1,
-5.799999999999999,
-5.499999999999998,
-5.199999999999998,
-4.899999999999999,
-4.599999999999998,
-4.299999999999997,
-3.9999999999999973,
-3.6999999999999975,
-3.399999999999997,
-3.099999999999996,
-2.7999999999999963,
-2.4999999999999964,
-2.1999999999999957,
-1.8999999999999955,
-1.5999999999999952,
-1.299999999999995,
-0.9999999999999951,
-0.6999999999999948,
-0.399999999999995,
-0.0999999999999952,
0.20000000000000462,
0.5000000000000047,
0.8000000000000047,
1.1000000000000045,
1.4000000000000046,
1.7000000000000046,
2.0000000000000044,
2.3000000000000047,
2.6000000000000045,
2.900000000000005,
3.2000000000000046,
3.5000000000000044,
3.8000000000000047,
4.100000000000005,
4.400000000000004,
4.700000000000005,
5.000000000000004,
5.300000000000005,
5.600000000000005,
5.900000000000006,
6.2000000000000055,
6.500000000000006,
6.800000000000006,
7.100000000000007,
7.400000000000007,
7.700000000000007,
8.000000000000007,
8.300000000000008,
8.600000000000007,
8.900000000000007,
9.200000000000008,
9.500000000000007,
9.800000000000008,
10.100000000000009,
10.40000000000001,
10.70000000000001,
11.000000000000009,
11.30000000000001,
11.60000000000001,
11.90000000000001,
12.20000000000001,
12.50000000000001,
12.800000000000011,
13.100000000000012,
13.400000000000011,
13.700000000000012,
14.00000000000001]
Als je bovenstaand voorbeeld runt, zou je een lijst met getallen moeten zien van -7 tot 14. Bedenk waarom, maak zelf de tabel handmatig (of met je GR) om te zien of de waarden een beetje kloppen.
Je zal net als hier wel eens ‘rare’ waarden zien zoals 6.20000000000055. Dat heet een floatingpoint error. Dat is een heel hoofdstuk apart, en komt door de manier waarop machines rekenen (getallen worden eerst in maximaal 58 0-en en 1-en opgeslagen en dan weer teruggehaald en dat gaat soms vreemd). Gaan we niet dieper op in, voor ons gebruik is de waarde gewoon 6.2. Vind je het interessant waar het vandaan komt, zoek dan op ‘floating point error’ en geniet.
Je ziet dat het best bewerkelijk is om iets simpels als een lijn te schrijven. Maar een groot voordeel is, nu we eenmaal de functie hebben gemaakt, hoeven we het nooit meer in dezelfde programma opnieuw te schrijven en halverwege op te roepen.
Opdracht 1#
Schrijf een functie genaamd parabool(a,b,c,xstart,xeind,stapgrootte), dat de functie f(x) = ax^2 +bx+c definieert.
Het kwadraat van een getal krijg je via x**2 of simpelweg x*x.
Roep vervolgens parabool(1, -6, 9, -5, 7, 0.01) op, dit is gelijk aan f(x) = x^2 -6x + 9 op interval [-5,7]
Grafieken plotten#
In python is het mogelijk om ook beeldbestanden aan te passen en te maken. In dit blok gaan we kennismaken met pyplot. Dat is een module die je eerst moet ‘installeren’ (aanroepen) aan het begin van je code EN kan hernoemen.
Dat doen we alsvolgt:
import matplotlib.pyplot as plt #importeer matplotlib en sla het op als variable plt
%matplotlib inline # dit zorgt ervoor dat afbeeldingen binnen dit scherm komen en niet als extern scherm pop uppen.
Als deze eenmaal is ‘gerund’ in dit python notebook, kan je met plt altijd een plot maken. We gaan de lijn plotten die we eerder hierboven hebben gemaakt. Dat ziet er dan als volgt uit, kijk naar de #opmerkingen voor wat elke regel nou eigenlijk doet.
import matplotlib.pyplot as plt
%matplotlib inline
def lijn(a,b,xstart,xeind,stapgrootte):
y=[xstart*a+b]
x=[xstart]
xwaarde = xstart
while xwaarde < xeind:
xwaarde = xwaarde+stapgrootte
ywaarde = a*xwaarde +b
x.append(xwaarde)
y.append(ywaarde)
return x,y
#LET OP, er is wat toegevoegd, behalve de y-waarden wil ik nu ook de x-waarden returnen. Als de functie is opgeroepen is hierna x gelijk aan het x-domein en y gelijk aan het y-bereik.
x,y=lijn(3,2,-3,4,0.1) #LET OP: hiermee sla je in x op de x-waarden uit de functiedefinitie hierboven en de y ook. met de komma kan je meerdere variabele in één regel opslaan. `x,y = 4,3` betekend voor x=4 en y=3
plt.figure(figsize=(10,10)) # hiermee geven we aan dat we een figuur willen maken van 10 bij 10. Hierin willen we een plot maken. Dit kan je weglaten, dan bepaald Python de grootte
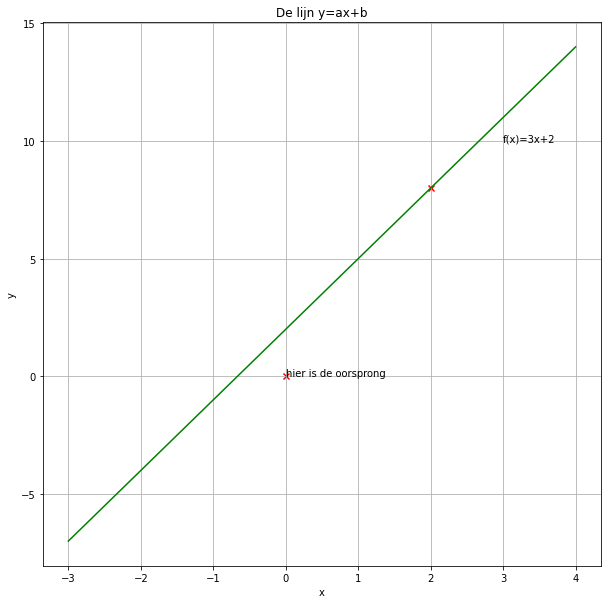
plt.plot(x, y, 'g-') # hierin wordt aangegeven WAT we willen plotten: wij willen horizontaal de x-waarden en verticaal de y-waarden. Daarna kan je de vorm van de grafiek aangeven: 'b-' geeft aan dat het een Blauwe lijn (-) moet zijn
plt.title('De lijn y=ax+b') # je kan een titel geven voor het hele diagram (hoeft niet per se bij wiskunde, bij natuurkunde vaak wel!)
plt.xlabel('x') # label je x-as. Bij wiskunde hebben we niet echt eenheden, bij natuurkunde zou er bijvoorbeeld tijd (s) kunnen staan
plt.ylabel('y') # label je y-as. Bij wiskunde hebben we niet echt eenheden, bij natuurkunde zou er bijvoorbeeld snelheid (m/s) kunnen staan
plt.scatter([0,2],[0,8],marker='x',c='r') # hiermee kan je losse punten toevoegen in dezelfde plot. Hier zet ik op (0,0) en op (2,8) een rood sterretje in de grafiek. Kan je doen als je bijvoorbeeld bijzondere punten wilt aangeven.
plt.text(0,0,'hier is de oorsprong') # hiermee kan je tekst toevoegen IN de grafiek. hier heb ik op (0,0) de tekst hier is de oorsprong toegevoegd.
plt.text(3,10,'f(x)=3x+2') # en nog een keer aanroepbaar, zodat ik ergens de lijn een naam kan geven (met functievoorschrift in mijn geval, hoef je niet altijd te doen)
plt.grid() # er moet een grid aangemaakt worden (lijntjes)
plt.show() # laat hieronder NU de grafiek dan zien.
EINDOPDRACHT#
Deze opdracht bestaat uit meerdere delen.
DEFINIEER een functie
oplossingenplotter(a,b,c)dat de oplossingen vana*x^2 +b*x+c =0teruggeeft en weergeeft in de plot. Denk na over bestaan van 0, 1 of 2 oplossingen en hoe dat uitgespuugd wordt door je functie. Gebruik hiertoe je uitwerking van de vorige opdracht.plot de grafiek van deze functie, en highlight met een markerking de (bijvoorbeeld met plt.scatter(…) ) de oplossingen. Zie als voorbeeld de ‘lijn’ helemaal bovenin hoe je dat aan kan pakken met de grootte van de assen EN het definieren van de x-waarden en y-waarden. Zorg dat rond de oplossingen geplot wordt (tip: als x1 de linker en x2 de rechter oplossing is, plot dan bijvoorbeeld op het interval [x1 - 1, x2 + 1]. ). Dit plotten gebeurd dus BINNEN de definitie nog (dat is makkelijker)
Voer dit uit met de functie oplossingenplotter(1, -6, 9) die de oplossingen plot van x^2 -6x + 9 = 0. Werk deze oplossing evt met de hand uit om te kijken of je programma correc werkt
Om je op weg te helpen hieronder het SKELET, maar zorg zelf voor de invulling en correcte uitwerking
import matplotlib.pyplot as plt
import numpy as np #dit voegen we nog even toe, om de wortel uit te kunnen rekenen als np.sqrt(getal)
%matplotlib inline
def oplossingenplotter(a,b,c):
... hier moet vast iets van een abc formule komen
if (een oplossing): #(wanneer had je eigenlijk ook alweer 0, 1 of 2 oplossingen)
x1=...
if (twee oplossingen):
x1=... en x2=... #wortel(D) np.sqrt(D) x^2 is x**2 of x*x
if (geen oplossingen):
#tja wat dan?
#dan wil je de functie gaan plotten, daartoe kan je de vorige opdracht 1 gebruiken voor het bouwen van de kwadratische functie. Die zou je hier ook kunnen aanroepen als je de functie boven al een keer gerudn hebt!
#Omdat je een grafiek wilt plotten zo 'glad mogelijk' wilt hebben, moet je de stapgrootte klein houden. Niet te klein, zoals 0.0000001, dan duurt het heel lang. 0.01 of 0.001 is meestal voldoende
